Breadth-First Search에서 경로를 추적하는 방법은 무엇입니까?
다음 예에서와 같이 Breadth-First Search의 경로를 어떻게 추적합니까?
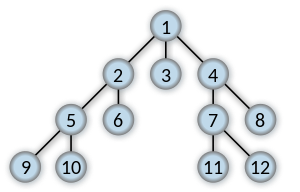
key를 검색하면 1에서 11까지 연결 11하는 가장 짧은 목록을 반환합니다 .
[1, 4, 7, 11]
먼저 http://en.wikipedia.org/wiki/Breadth-first_search를 봐야 합니다.
아래는 목록 목록을 사용하여 경로 대기열을 나타내는 빠른 구현입니다.
# graph is in adjacent list representation
graph = {
'1': ['2', '3', '4'],
'2': ['5', '6'],
'5': ['9', '10'],
'4': ['7', '8'],
'7': ['11', '12']
}
def bfs(graph, start, end):
# maintain a queue of paths
queue = []
# push the first path into the queue
queue.append([start])
while queue:
# get the first path from the queue
path = queue.pop(0)
# get the last node from the path
node = path[-1]
# path found
if node == end:
return path
# enumerate all adjacent nodes, construct a new path and push it into the queue
for adjacent in graph.get(node, []):
new_path = list(path)
new_path.append(adjacent)
queue.append(new_path)
print bfs(graph, '1', '11')
또 다른 접근 방식은 각 노드에서 부모로의 매핑을 유지하고 인접 노드를 검사 할 때 부모를 기록하는 것입니다. 검색이 완료되면 상위 매핑에 따라 역 추적하면됩니다.
graph = {
'1': ['2', '3', '4'],
'2': ['5', '6'],
'5': ['9', '10'],
'4': ['7', '8'],
'7': ['11', '12']
}
def backtrace(parent, start, end):
path = [end]
while path[-1] != start:
path.append(parent[path[-1]])
path.reverse()
return path
def bfs(graph, start, end):
parent = {}
queue = []
queue.append(start)
while queue:
node = queue.pop(0)
if node == end:
return backtrace(parent, start, end)
for adjacent in graph.get(node, []):
if node not in queue :
parent[adjacent] = node # <<<<< record its parent
queue.append(adjacent)
print bfs(graph, '1', '11')
위의 코드는 사이클이 없다는 가정을 기반으로합니다.
I liked qiao's first answer very much! The only thing missing here is to mark the vertexes as visited.
Why we need to do it?
Lets imagine that there is another node number 13 connected from node 11. Now our goal is to find node 13.
After a little bit of a run the queue will look like this:
[[1, 2, 6], [1, 3, 10], [1, 4, 7], [1, 4, 8], [1, 2, 5, 9], [1, 2, 5, 10]]
Note that there are TWO paths with node number 10 at the end.
Which means that the paths from node number 10 will be checked twice. In this case it doesn't look so bad because node number 10 doesn't have any children.. But it could be really bad (even here we will check that node twice for no reason..)
Node number 13 isn't in those paths so the program won't return before reaching to the second path with node number 10 at the end..And we will recheck it..
All we are missing is a set to mark the visited nodes and not to check them again..
This is qiao's code after the modification:
graph = {
1: [2, 3, 4],
2: [5, 6],
3: [10],
4: [7, 8],
5: [9, 10],
7: [11, 12],
11: [13]
}
def bfs(graph_to_search, start, end):
queue = [[start]]
visited = set()
while queue:
# Gets the first path in the queue
path = queue.pop(0)
# Gets the last node in the path
vertex = path[-1]
# Checks if we got to the end
if vertex == end:
return path
# We check if the current node is already in the visited nodes set in order not to recheck it
elif vertex not in visited:
# enumerate all adjacent nodes, construct a new path and push it into the queue
for current_neighbour in graph_to_search.get(vertex, []):
new_path = list(path)
new_path.append(current_neighbour)
queue.append(new_path)
# Mark the vertex as visited
visited.add(vertex)
print bfs(graph, 1, 13)
The output of the program will be:
[1, 4, 7, 11, 13]
Without the unneccecery rechecks..
I thought I'd try code this up for fun:
graph = {
'1': ['2', '3', '4'],
'2': ['5', '6'],
'5': ['9', '10'],
'4': ['7', '8'],
'7': ['11', '12']
}
def bfs(graph, forefront, end):
# assumes no cycles
next_forefront = [(node, path + ',' + node) for i, path in forefront if i in graph for node in graph[i]]
for node,path in next_forefront:
if node==end:
return path
else:
return bfs(graph,next_forefront,end)
print bfs(graph,[('1','1')],'11')
# >>>
# 1, 4, 7, 11
If you want cycles you could add this:
for i, j in for_front: # allow cycles, add this code
if i in graph:
del graph[i]
Very easy code. You keep appending the path each time you discover a node.
graph = {
'A': set(['B', 'C']),
'B': set(['A', 'D', 'E']),
'C': set(['A', 'F']),
'D': set(['B']),
'E': set(['B', 'F']),
'F': set(['C', 'E'])
}
def retunShortestPath(graph, start, end):
queue = [(start,[start])]
visited = set()
while queue:
vertex, path = queue.pop(0)
visited.add(vertex)
for node in graph[vertex]:
if node == end:
return path + [end]
else:
if node not in visited:
visited.add(node)
queue.append((node, path + [node]))
I like both @Qiao first answer and @Or's addition. For a sake of a little less processing I would like to add to Or's answer.
In @Or's answer keeping track of visited node is great. We can also allow the program to exit sooner that it currently is. At some point in the for loop the current_neighbour will have to be the end, and once that happens the shortest path is found and program can return.
I would modify the the method as follow, pay close attention to the for loop
graph = {
1: [2, 3, 4],
2: [5, 6],
3: [10],
4: [7, 8],
5: [9, 10],
7: [11, 12],
11: [13]
}
def bfs(graph_to_search, start, end):
queue = [[start]]
visited = set()
while queue:
# Gets the first path in the queue
path = queue.pop(0)
# Gets the last node in the path
vertex = path[-1]
# Checks if we got to the end
if vertex == end:
return path
# We check if the current node is already in the visited nodes set in order not to recheck it
elif vertex not in visited:
# enumerate all adjacent nodes, construct a new path and push it into the queue
for current_neighbour in graph_to_search.get(vertex, []):
new_path = list(path)
new_path.append(current_neighbour)
queue.append(new_path)
#No need to visit other neighbour. Return at once
if current_neighbour == end
return new_path;
# Mark the vertex as visited
visited.add(vertex)
print bfs(graph, 1, 13)
The output and everything else will be the same. However, the code will take less time to process. This is especially useful on larger graphs. I hope this helps someone in the future.
참고URL : https://stackoverflow.com/questions/8922060/how-to-trace-the-path-in-a-breadth-first-search
'program story' 카테고리의 다른 글
| 작업 실행시 AWS ECS 오류 : 클러스터에 컨테이너 인스턴스가 없습니다. (0) | 2020.09.07 |
|---|---|
| Windows 명령 프롬프트에서 꺾쇠 괄호 이스케이프 (0) | 2020.09.07 |
| Android Studio 게스트가 7 초 내에 온라인 상태가되지 않습니다. (0) | 2020.09.07 |
| ConcurrentLinkedQueue를 사용하는 방법? (0) | 2020.09.07 |
| jQuery의 이벤트 핸들러에 인수를 어떻게 전달할 수 있습니까? (0) | 2020.09.07 |